For the passion of revealing stories in relational data
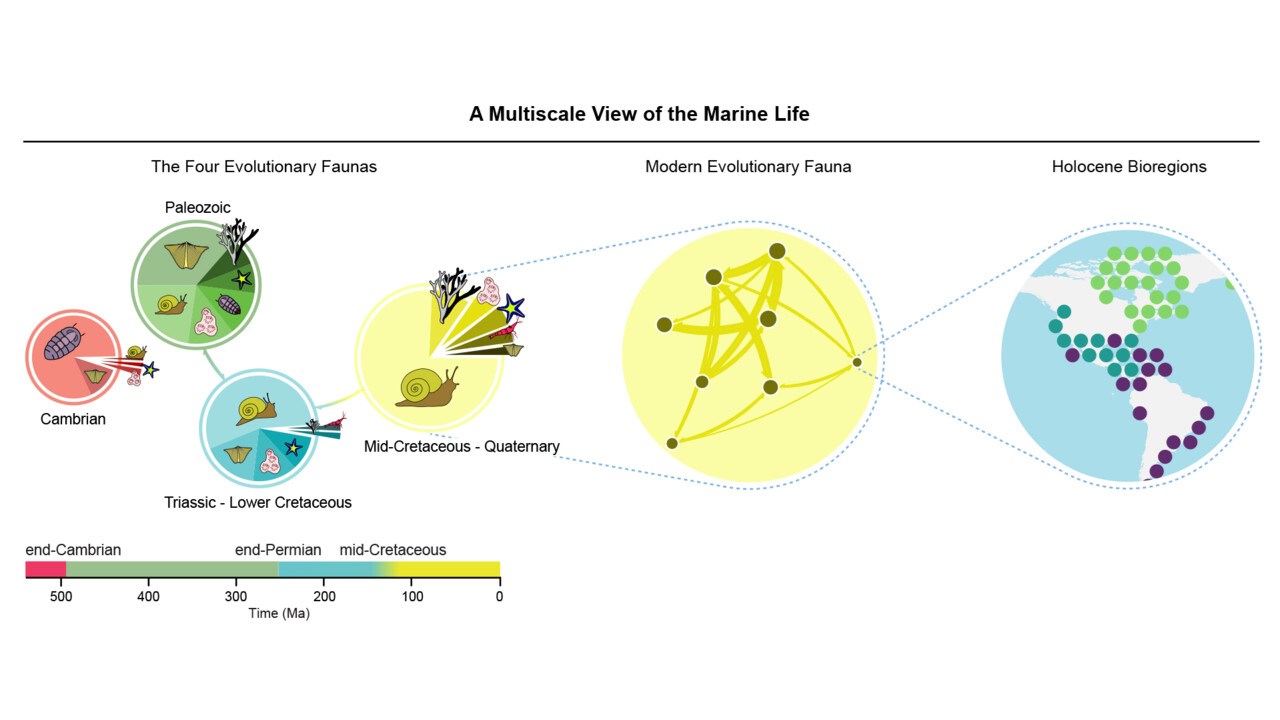
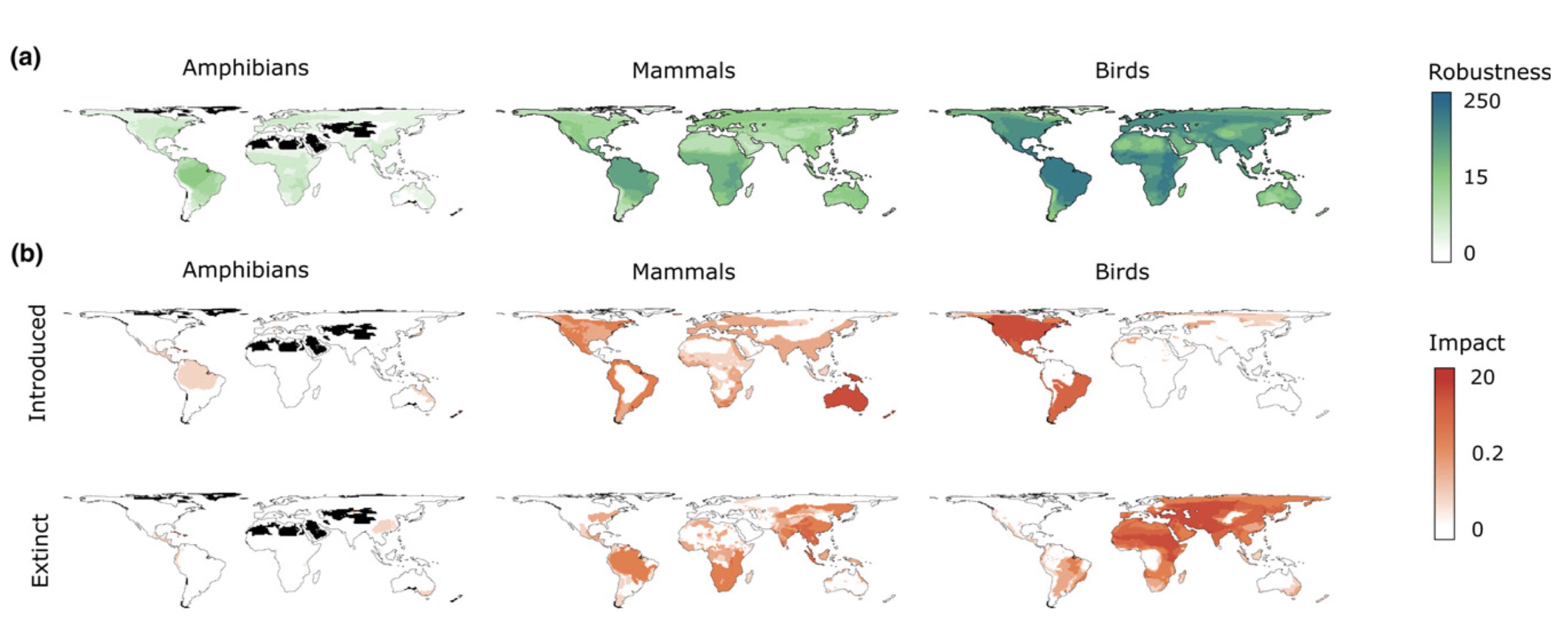
We study information flows through social and biological systems to comprehend their inner workings. By simplifying myriad network interactions into maps of significant information flows, we can address research questions about how diseases spread, plants respond to stress, and life distributes on Earth. Our goal is to generate reliable predictions and suggest successful strategies to secure a sustainable future.

My work and interests

Maps of networks
Want to transform raw relational data into insightful maps and discoveries? Simplify and highlight important structures in networks with our tools available on mapequation.org

Helping businesses love their data
I am co-founder of Infobaleen together with Daniel Edler, Andrea Lancichinetti, Niklas Lovén, Christian Persson, and Jakob Sjölander. Infobaleen…

My journey in life and science
My life is an improv dance with family, cross-country skiing, outdoor fun, and research. I was born in Uppsala…

Welcome to IceLab!
I am a professor of physics with focus on computational science. You find me in Integrated Science Lab, IceLab, on…